Algoritma Bressenhem
·
Prosedur untuk
menggambar kembali garis dengan membulatkan nilai x atau y kebilangan integer
membutuhkan waktu, serta variable x,y dan m merupakan bilangan real karena
kemiringan merupakan nilai pecahan
·
Bressenham
mengembangkan algoritma klasik yang lebih menarik, karena hanya menggunakan
perhitungan matematika dengan bilangan integer
·
Dengan demikian
tidak perlu membulatkan nilai posisi setiap pixel setiap waktu
·
Algoritma garis
Bressenhem disebut juga midpoint line algorithm adalah algoritma konversi
penambahan nilai integer yang juga dapat diadaptasi untuk menggambar sebuah
lingkaran.
Langkah-langkah untuk
membentuk garis menurut algoritma bressenhem adalah :
• Tentukan
dua titik yang akan dihubungkan dalam pembentukan garis.
• Tetukan
salah satu titik disebelah kiri sebagai titik awal (x0, y0 ) dan titik lainnya
sebagai titik akhir (x1, y1 ).
• Hitung
∆x, ∆y, 2∆x, dan 2∆y – 2∆x.
• Hitung
parameter p0 = 2∆y –2∆x.
• Untuk
setiap xk sepanjang jalur garis, dimulai dengan k = 0
• bila
pk < 0 maka titik selanjutnya (xk+1,yk) dan Pk+1=pk+2∆y
• Bila
tidak maka titik selanjutnya adalah
(Xk+1,Yk+1) dan Pk+1=Pk+ 2∆y-2∆x
• Ulangi langkah nomor 5 untuk menentukan posisi pixel
selanjutnya, sampai x = x1 dan y = yk.
Contoh
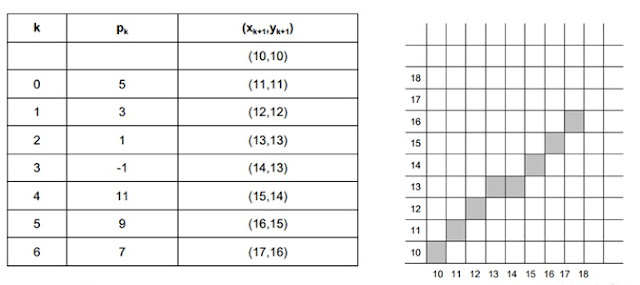
• Untuk menggambarkan algoritma Bressenham dalam
pembentukan suatu garis yang menghubungkan titik (10,10) dan (17,16),
pertama-tama ditentukan bahwa titik (10,10) berada disebelah kiri merupakan
titik awal, sedangkan (17,16) merupakan titik akhir. Posisi yang membentuk
garis dapat ditentukan dengan perhitungan sebagai berikut :
• ∆x=x1-x0 dan ∆y=y1-y0
• ∆x=17-10=7, ∆y=16-10=6
• Parameter P0=2 ∆y- ∆x
• P0=(2x6)-7 = 5
• Increment : 2 ∆y=12 à2 ∆y- 2∆x=12-14=-2
Px=3
à
pk+1=pk+2Dy-2DX= 5+ -2 = 3
Quiz
- Buat sebuah garis yang menghubungkan dari titik (20,10) sampai dengan titik (30,18) dengan menggunakan algoritma Bressenham. (Uraikan langkahnya)
Jawabanya
• ∆x=x1-x0 dan ∆y=y1-y0
• ∆x=30-20=10, ∆y=18-10=8
• Parameter P0=2 ∆y- ∆x
• P0/PK=(2x8)-10 = 6
• Increment : 2 ∆y=16 à2
∆y- 2∆x=16-20=-4
|
K
|
PK
|
( Xk+1, Yk+1)
|
|
|
|
20,10
|
|
0
|
6
|
21,11
|
|
1
|
2
|
22,12
|
|
2
|
-2
|
23,12
|
|
3
|
14
|
24,13
|
|
4
|
10
|
25,14
|
|
5
|
6
|
26,15
|
|
6
|
2
|
27,16
|
|
7
|
-2
|
28,16
|
|
8
|
14
|
29,17
|
|
9
|
10
|
30,18
|
Grafik Kalkulator :



Komentar
Posting Komentar